Shaokang's Blog

This project is a group work designed and solve by Shaokang Jiang & Katherine Fu for course CS524 project.

Optimization is a powerful way to solve real problem in a short amount of time. It needs us to use more math when we design solutions instead of using computing resources when the problem runs. GAMS is a powerful optimization software. GAMS could do calculation and generate equations in seconds. By using CPLEX, we are able to reach solutions in seconds. In this project, we utilize GAMS feature (dynamic sets, mip, etc) and nearly solved a real problem.

Problem

College library optimization problem

We consider a simplified example of arranging the number of students who use the college library for studying. In different period of time during school year, the number of students staying in the library is different. During the midterm and final weeks, the number is rapidly increasing. Thus, it is essential to maximize the efficiency of the number of hours of students who can use the library given their studying duration of using individual seats, the inflow and outflow of students, the equipment checking-out situations, and so on.

To simplify our model, we assume that the library has two sections: a quiet area, a public area. The total number of seats in the college library is 1000.

Quiet area
Public area
≤5 hrs>5 hrsFor projectFor chatting
≤2 hrs>2 hrs≤4 hrs>4 hrs
10.61.10.50.120.05

To understand the Efficiency, we gave an example at here. Assume a person could finish a page of work in an hour, this is defined as one unit of efficiency, also known as the efficiency per hour for a person work in quiet area for less than 5 hours. But if this person work more than 5 hours, then he/she can only finish 0.6 pages of work for each hour he/she spend. By using formula, it looks like this: (t stand for time of working, f(t) stand for total efficiency) Equation 1 stand for student total efficiency staying in quiet area. Equation 2 stand for student total efficiency staying in public area for project purpose. Equation 3 stand for student total efficiency staying in public area for chatting purpose.

\begin{equation} f(t)=\left\{ \begin{aligned} & 1*t & \forall t\le 5 \\ & 5+0.6*t & \forall t> 5 \end{aligned} \right. \end{equation} \begin{equation} f(t)=\left\{ \begin{aligned} & 1.1*t & \forall t\le 2 \\ & 2.2+0.5*t & \forall t> 2 \end{aligned} \right. \end{equation} \begin{equation} f(t)=\left\{ \begin{aligned} & 0.12*t & \forall t\le 4 \\ & 0.48+0.05*t & \forall t> 4 \end{aligned} \right. \end{equation}

It is permitted to switch a person from quiet place to public place. A person who requested the quiet apace and switched to public space due to limited seats will have an coefficient of efficiency of 0.8; A person who requested the public apace and switched to quiet space due to limited seats will have an coefficient of efficiency of 0.3;

Equation below stand for student total efficiency. (x represent for the original efficiency this student have, which is also the caalculation result from the previous step, f(x) stand for result of new efficiency)

\begin{equation} f(x)=\left\{ \begin{aligned} & 0.8*x & \forall x| quiet\rightarrow public \\ & 0.3*x & \forall x| public \rightarrow quiet \end{aligned} \right. \end{equation}

The college library also provides equipment including laptops,
calculators, and computer chargers for students to use. If a student
checks out one of these equipment, the efficiency of that student could be multiply by those coefficient. The coefficient for regular efficiency is shown below.

Laptopscalculatorscomputer chargers
1.11.21.3

Equation below stand for student total efficiency. (x represent for the original efficiency this student have, which is also the calculation result from the previous step, f(x) stand for result of new efficiency)

\begin{equation} f(x)=\left\{ \begin{aligned} & 1.2*x & \forall x| calculator=1 &\\ & 1.1*x & \forall x| laptops=1 &\\ & 1.3*x & \forall x| charger=1 & \end{aligned} \right. \end{equation}

The number of laptops is 10, the total number of calculators is 30, and
the number of chargers is also 10. Every person could use those equipment for the time duration that they are study in the library. Each person could borrow at most one equipment during time duration that he is in library.

data.gdx contain the data of students’ thinking of purpose of using those equipment and seats in the library. We want to consider a situation in a day of experimenting period during opening hours of 8:00 am to 9:00 pm. This file recorded the time when a student enter the library; the time they want to study; the place they want to study; Max possible hours for quiet hours is 10. Max possible hours for public hours is 6; type of 0 stands for project, 1 stands for chatting;

By using data above, you are going to give permission for certain group of students to enter this library and arrange seats in the library in order to maximize total efficiency. And also, to demonstrate that this library is open to all people, you get to allow at least 10 chatting people to enter this library.

Objective1:

How to arrange seats in the library to try the best to meet the requirement of student’s thought in data.gdx and maximize the total efficiency of students using the library? Also, which student will be permitted of entering this library?

Dataset could be downloaded from data.gdx.

Objective2:

More gdx file is provided. Those gdx files describe different time of requests from students. How to arrange seats in the library to try the best to meet the requirement of student’s thought in those gdx files and maximize the total efficiency of students using the library? Each gdx file is considered as a different scene, store the output in parameter and plot different seat arrangement during this year in a line diagram and draw out if there is any suggestion to provide to the library.

Dataset could be downloaded from data-free.gdx, data-middle.gdx, data-busy.gdx.

Objective3:

Solve the model multiple times with different total seats provided, do you have any recommendation for the school that they need to buy more seats or not? Do not consider rules of fire protection design and construction of buildings. Plot the result in graph and explain the reason.

Analyze:

The approach used.

We organized the requests from all the students based on their (enter_hour, public_hour) with the help of variables, respectively, n_pe_public and n_pe_quiet. These are represented as the maxmize number of people each regetangle block could contain in the graph below.

Diagram

Regarding the opening time of the library, there are two variables called quiet_arrange and public_arrange in a form of tuples (enter_hour, public_hour) as an entry. Based on the graph above, every quiet(open_hour, quiet_hour) variable contains # of people staying on seat at certain time interval and the duration of his or her studying hours is illustrated as the length of each block. Same case for public area. After we synthesized all the cases of students from his or her entering times to leaving times, we could form a complete diagram and the left graph above is a snippet.

In general, we utilized a dynamic set determined by students’ entering time and the duration of studying in either quiet or public area during each time interval from 8 am to 9 pm to measure the seat arrangement. This dynamic dataset is called “visible_quiet”, a 3-dimensional set, with sets (o, enter_hour, quiet_hour). It means, for every time interval o(as 10:00 in above) starting from 8 am, the (open_hour, quiet_hour) should be counted once, which is shown as shaded blocks on the top right side. In each time interval, a decent amount of students will enter the library and the total number during that time will be calculated. For example, based on the graph above, quiet(“8”, “3”) records the number of students who enter the library at 8 am and stay for 3 hours. If another student comes at 10 am and has also studied for 3 hours, we should count both of them in the time interval from 10 am to 11 am (the shaded area). The sum of number of students that shaded blocks contains should be less or equal to a corresponding variable(called quiet_chairs in code). Similiar case would be applied to public case.

We also took the seat-switching situations as considerations. The number of students in quiet area in certain interval should be the sum of the number of current students, those who just arrive, and those who switch from the public area to the quiet area(named as switch_p2q in code). Same thing applies to the arrangement of the public area(in a variable called switch_q2p).

Our objective is to maximize the total efficiency. We realized the utilization of calculators, chargers and laptops will also exert significant effects on students’ efficiency. Considering that it was hard to calculate them with our original model, we splited the entire block into two stages demonstrated in two blocks in obj1. The first stage begin from the head of introduction and end at here. Because we had them in the problem description part, we solved the second stage and use this model to discover data in obj2. In the first stage, the model is calculated by multiplying the base total efficiency coefficients with the number of hours students spend in each area. The base total efficiency coefficients depend on area and hours, so they are pre-calculated and stored in eff_quiet and eff_public in the code. We also considered the situation whether students switch areas or utilize equipments. For different scenarios, we multiplied hours with different coefficients. More details will be discussed in the section below.

For the second stage of the problem, we employed some variables similar to ca_need_public, ca_need_quiet to represent the machines borrowed at pair (enter_hour, quiet_hour). We organized the needs for devices at first and set up them as an upper bound. The other procedures are similar to methods using in stage one. One difference is that we utilized some variableS for spliting, similar to ca_need_public_1, ca_need_public_2. They are used later for the objective function. Because the objective function has two variables with different conditions(quiet_arrange and switch_p2q) in each type(pblic or quiet) taking different final coefficient, we need to split the variable to represent those conditions. Because we try to maximizing the problem, the program will always fill the quiet_arrange first as it has a higher coefficient in general.

In terms of the number of equipments, we assumed that the requests for equipments should be greater than the number the library has. Given a simple example. If four students all require to use calculator but currently, the library only has 3 calculators available, we try to find a way to give the calculators to students in order to maximize the total efficiency.

Optimization model

We first counted the total number of people in either public or private areas based on the avalibility. Then, we calculated the efficiency of both regular studying hour, switching situations, and, equipment check-out situations and attempt to maxmize the total efficiency. We finally displayed students who have been chosen to study in certain seats in certain time interval.

We simplified the representation so we only represented the quiet study room and calculator case.
In the model, we had those variables:

  • let o to be a set of open hour from 8 to 21.
  • let q to be a set of people can stay in the quiet room, from 1 to 10.
  • let ty be the type of public object, it could be chat or project.
  • let qi be the set of original people record identity number, and cj be the category, like enter, hours, calculator
  • Let QuietmlQuiet_{ml} for m∈qi,l∈cjm\in qi, l\in cj represent the dataset.
  • let sqijksq_{ijk} for i,j∈o,k∈qi,j\in o, k\in q be the dynamic set represents at hour i, people who come in at j and plan to stay k hours, which is visible. For example, s9jks_{9jk} = {(8,2),(8,3),(8,4)…(8,10),(9,1),(9,2),(9,3)…(9,10)}
  • let splijksp_{lijk} for l∈ty,i,j∈o,k∈ql\in ty, i,j\in o, k\in q be the dynamic set represents at hour i, people who come in at j and plan to stay k hours, which is visible. For example, s19jks_{19jk} = {(8,2),(8,3),(8,4)…(8,6),(9,1),(9,2),(9,3)…(9,6)}
  • let EkE_{k} for k∈qk\in q to be the Base total efficiency base vector on time k.
  • let P2QljkP2Q_{ljk} for l∈ty,j∈o,k∈ql\in ty, j\in o, k\in q to be people switch from public area to quiet area enter at hour j and stay for hours k. Same mechanism for Q2PQ2P
  • let variable QCQC be the chairs should be in quiet room.
  • let variable QjkQ_{jk} for j∈o,k∈qj\in o, k\in q be the number of people accepted to the library to maximize total efficiency
  • let variable CQ1jkCQ1_{jk} for j∈o,k∈qj\in o, k\in q be the number of calculator split for quiet area accepted to the library to maximize total efficiency
  • let variable CQ2jkCQ2_{jk} for j∈o,k∈qj\in o, k\in q be the number of calculator accepted to the library to maximize total efficiency
  • let CFCF be the increment factor of efficiency of using calculator, let SWPQSWPQ be the factor of efficiency of switch from public to quiet
  • Let NPQjkNPQ_{jk} for j∈o,k∈qj\in o, k\in q be the number of people requested to stay in the library.
  • Let NCQjkNCQ_{jk} for j∈o,k∈qj\in o, k\in q be the number of calculator requested to stay in the library.
  • Let SQmSQ_{m} for m∈qim\in qi be a binary variable record which people is selected
  • Let SQCmSQC_{m} for m∈qim\in qi be a binary variable record which people has calculator

Max∑k∈qEkT(∑j∈o(Qjk+CQ1jk∗CF+(∑l∈tyP2Qljk+CQ2jk∗CF)∗SWPQ))Max \sum_{k\in q}E_{k}^T(\sum_{j\in o}(Q_{jk}+CQ1_{jk}*CF+(\sum_{l\in ty}P2Q_{ljk}+CQ2_{jk}*CF)*SWPQ))

\begin{align} \begin{split} s.t.\quad & CQ1_{jk} + CQ2_{jk} \le NCQ_{jk} && \forall j\in o,k\in q \\ & Q_{jk} \le NPQ_{jk}&&\forall j\in o,k\in q\\ & 1000\ge QC&\\ & \sum_{j,k}Q_{jk}+\sum_{l,j,k}P2Q_{ljk}\le QC &&\forall i\in o, \forall Q_{jk}\in sq_{ijk}, \forall P2Q_{ljk}\in sp_{ijk} \\ & \sum_{m\in qi} SQ_{m} = Q_{jk}&& \forall j\in o, k\in q,\forall m\in \{m | Quiet_{m"enter"}=j\\ &&& \&Quiet_{m"hours"}=k\}\\ & \sum_{m\in qi} SQC_{m} \ge CQ1_{jk} + CQ2_{jk} && \forall j\in o, k\in q,\forall m\in \{m | Quiet_{m"enter"}=j\\ &&& \&Quiet_{m"hours"}=k\& Quiet_{m"Calculator"}=1\}\\ & \sum_{j,k}(CQ1_{jk} + CQ2_{jk})\le 20 &&\forall i\in o, \forall CQ1_{jk}, CQ2_{jk}\in sq_{ijk} \\ & CQ1_{jk} \le Q_{jk}+Q2P_{jk}&&\forall i\in o, k\in q \end{split} \end{align}

Most of other formulas for the entire project is similiar to the methods using above, so we choose to not write them.

For the solutions, see here for solution of obj1, here for solution of obj2, here for solution of obj3

Processing of the solution


processing for the first objective


processing for the second objective


processing for the third objective

Some brief conclusion


As shown in area below

Conclusion for the first objective
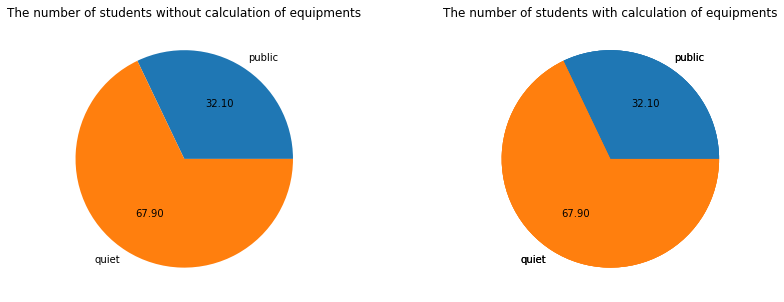
Based on our problem, (the total_limit is 1000), there are no significant difference between borrowing equipments and not borrowing equipments. But if we look into a smaller scalar problem, there are difference betweeen those two cases. The reason for it is that borrowing equipment has a low chance to happen.

For the conclusion, library need to arrange 321 seats for public area and 679 seats for quiet area in order to maxmize students’ total efficiency in the busy hours. We also demostrate a permission list but we think it is not unique and it is not as important as seats arrangement. So, we represented it but not discuss a lot about it.


Conclusion for the second objective
As we mentioned in the problem, we provided the permission in each case. But it is not useful.

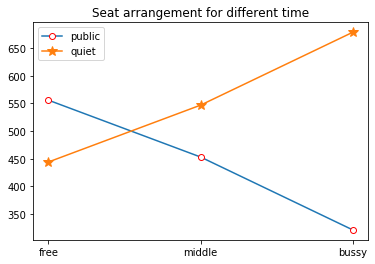
By using the graph, we could clearly see that more quiet seats need to be arranged when students get bussier. This might be a guidance for library to provide different arrangement of seats in different time period.


Conclusion for the third objective
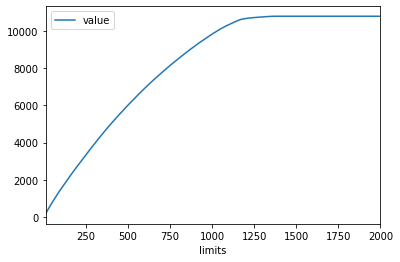
As we could see on the graph that the slope goes down at point around 1200. So for the bussiest season, school do need to buy more chairs for students to study.


Conclusion for the entire objective
As we could see on the graph that the slope goes down at point around 1200. So for the bussiest season, school do need to buy more chairs for students to study.

Further thoughts:


Furthermore, there are lots of improvements that could be done.

  • Since our model separates the public and quiet areas in our parameter, it is hard for us to simplify our model. In the future model, we could try to combine these two into one parameter to make it simplier.

  • The constraints, dealing ways might need to be improved. And there might be some small errors as there are too many equations. We checked them for multiple times, but it is hard to guarantee that every place is perfectly correct.

  • And the model could only make sense if they have the real data input. Right now, we only have fake data.

  • Solution is not unique(for selection of people). Maybe we don’t have to find which person should be given the permission. We could find the number of people we should accept in each case.

  • we always want to keep minimum change to what we setup in the previous submission, A lot of places could be improved actually. Like obj2, execute_load command would be better.

  • like what we discussed in obj3, some more discoveries could be done, including if the library needs to buy more calculators or not.

  • And, not all people are on time in real case. In this problem, we assume data are collected from survey or somethimg. So, there is no person would have a time duration of 2:15. But in real case, this would happen. So, it would be helpful to invite error vectors to describe this and form the problem.

Solution:

Important startup of jupyter notebook interface:

1
2
3
4
5
6
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:95% !important; }</style>"))
# Load the gams extension
%load_ext gams_magic
%matplotlib inline
from matplotlib import pyplot as plt

Objective1:

How to arrange seats in the library to try the best to meet the requirement of student’s thought in data.gdx and maximize the total efficiency of students using the library? Also, which student will be permitted of entering this library?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
%%gams 
* initialize data
$title College library optimization problem     Katherine Fu & Shaokang Jiang
set public_i, public_j, quiet_i, quiet_j, hours /1*10/, public_hour(hours) /1*6/, quiet_hour(hours) /1*10/, enter_hour /8*20/, types "1:project 2:chatting" /1*2/;
alias(enter_hour, o);
parameter
    Public(public_i,public_j),
    Quiet(quiet_i,quiet_j)
    n_pe_public(types, enter_hour, public_hour)
    n_pe_quiet(enter_hour, quiet_hour)
    eff_public(types, public_hour)
    eff_quiet(quiet_hour);
option optcr = 0;
$gdxin data.gdx
$load public_i<Public.dim1 public_j<Public.dim2 Public=Public
$load quiet_i<Quiet.dim1 quiet_j<Quiet.dim2 Quiet=Quiet
$gdxin
scalar total_limit /1000/, chat_low /10/, q2p "switch efficiency factor" /0.8/, p2q "switch efficiency factor" /0.3/;

* dynamic set of visibility
set visible_public(o, enter_hour, public_hour) "For entity at o, (enter_hour, public_hour) are accessible nodes, mean # of ppl sit on it"
    visible_quiet(o, enter_hour, quiet_hour) "For entity at o, (enter_hour, public_hour) are accessible nodes, mean # of ppl sit on it";
visible_public(o, enter_hour, public_hour) = yes$(ord(o)<ord(enter_hour)+ord(public_hour) and ord(o)>=ord(enter_hour));
visible_quiet(o, enter_hour, quiet_hour) = yes$(ord(o)<ord(enter_hour)+ord(quiet_hour) and ord(o)>=ord(enter_hour));

* calculate the base total efficiency for each (enter_hour, quiet_hour)
eff_public("1", public_hour) = (1.1*ord(public_hour))$(ord(public_hour)<=2) + (1.2+0.5*ord(public_hour))$(ord(public_hour)>2);
eff_public("2", public_hour) = (0.12*ord(public_hour))$(ord(public_hour)<=4) + (0.28+0.05*ord(public_hour))$(ord(public_hour)>4);
eff_quiet(quiet_hour) = (ord(quiet_hour))$(ord(quiet_hour)<=5) + (2+0.6*ord(quiet_hour))$(ord(quiet_hour)>5);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
%%gams
* declare variables for first model to use
integer variables public_chair "# of chairs for public area", quiet_chair "# of chairs for quiet area",
            public_arrange(types, enter_hour, public_hour) "# of chairs for types for public area at hour enter_hour and stay at here for public_hour",
            quiet_arrange(enter_hour, quiet_hour) "# of chairs for quiet area at hour enter_hour and stay at here for quiet hour"
            switch_q2p(enter_hour, quiet_hour) "# of chairs switched from quiet area to public area"
            switch_p2q(types, enter_hour, public_hour) "# of chairs switched from public area to quiet area";
public_chair.up = total_limit;
quiet_chair.up = total_limit;
public_arrange.up(types, enter_hour, public_hour) = total_limit;
quiet_arrange.up(enter_hour, quiet_hour) = total_limit;
switch_q2p.up(enter_hour, quiet_hour) = total_limit;
switch_p2q.up(types, enter_hour, public_hour) = total_limit;
free variable total_efficiency;
binary variable select_public(public_i), select_quiet(quiet_i);

* calculate total number of people
n_pe_public(types, enter_hour, public_hour) = sum(public_i, 1$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
n_pe_quiet(enter_hour, quiet_hour) = sum(quiet_i, 1$((Quiet(quiet_i,"enter") = 7+ord(enter_hour)) and (Quiet(quiet_i,"hours") = ord(quiet_hour))));

equations conn1 "connection between public_chair and public_arrange and switch_q2p at every time"
          conn2 "connection between quiet_chair and quiet_arrange and switch_p2q"
          objective "Calculate the total efficiency"
          limit "limitation of total chairs"
          people_public "restriction of # of people in public area"
          people_quiet "restriction of # of people in quiet area"
          selection_public "people selected at public area"
          selection_quiet "people selected at quiet area"
          chatting_lower "Hold constraints for the lower limitation for chatting people";
conn1(o)..
    sum((types, enter_hour, public_hour), public_arrange(types, enter_hour, public_hour)$visible_public(o, enter_hour, public_hour)) + sum((enter_hour, quiet_hour), switch_q2p(enter_hour, quiet_hour)$visible_quiet(o, enter_hour, quiet_hour)) =l= public_chair;
conn2(o)..
    sum((enter_hour, quiet_hour), quiet_arrange(enter_hour, quiet_hour)$visible_quiet(o, enter_hour, quiet_hour)) + sum((types, enter_hour, public_hour), switch_p2q(types, enter_hour, public_hour)$visible_public(o, enter_hour, public_hour)) =l= quiet_chair;
limit..
    total_limit =g= public_chair + quiet_chair;
objective..
    total_efficiency =e= sum((types, enter_hour, public_hour), public_arrange(types, enter_hour, public_hour)*eff_public(types, public_hour) + switch_p2q(types, enter_hour, public_hour)*eff_public(types, public_hour)*p2q) +
                         sum((enter_hour, quiet_hour), quiet_arrange(enter_hour, quiet_hour)*eff_quiet(quiet_hour) + switch_q2p(enter_hour, quiet_hour)*eff_quiet(quiet_hour)*q2p);
people_public(types, enter_hour, public_hour)..
    public_arrange(types, enter_hour, public_hour) + switch_p2q(types, enter_hour, public_hour) =l= n_pe_public(types, enter_hour, public_hour);
people_quiet(enter_hour, quiet_hour)..
    quiet_arrange(enter_hour, quiet_hour) + switch_q2p(enter_hour, quiet_hour) =l= n_pe_quiet(enter_hour, quiet_hour);
selection_quiet(enter_hour, quiet_hour)..
    sum((quiet_i)$(Quiet(quiet_i,"enter")=7+ord(enter_hour) and Quiet(quiet_i,"hours")=ord(quiet_hour)), select_quiet(quiet_i)) =e= quiet_arrange(enter_hour, quiet_hour) + switch_q2p(enter_hour, quiet_hour);
selection_public(types, enter_hour, public_hour)..
    sum((public_i)$(Public(public_i,"type")=ord(types)-1 and Public(public_i,"enter")=7+ord(enter_hour) and Public(public_i,"hours")=ord(public_hour)), select_public(public_i)) =e= switch_p2q(types, enter_hour, public_hour) + public_arrange(types, enter_hour, public_hour);
chatting_lower..
    sum((enter_hour, public_hour), public_arrange("2", enter_hour, public_hour)) =g= chat_low;
model simple_obj1 /conn1, conn2, limit, objective, people_public, people_quiet, selection_quiet, selection_public, chatting_lower/;
solve simple_obj1 using mip maxmizing total_efficiency;

set run /1*2/, room /public, quiet/;
parameter selection_quiet_(run, quiet_i), selection_public_(run, public_i), chairs(run, room);
selection_public_("1", public_i) = select_public.l(public_i);
selection_quiet_("1", quiet_i) = select_quiet.l(quiet_i);
chairs("1", "public") = public_chair.l; 
chairs("1", "quiet") = quiet_chair.l;
Solver StatusModel StatusObjective#equ#varModel TypeSolverSolver Time
0Normal (1)Optimal Global (1)9699.1486014403MIPCPLEX0.038

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
%%gams
* increment of scalar for each factor
scalar calculator_factor /0.2/, laptop_factor /0.1/, charger_factor /0.3/, calculators /30/, laptops /10/, chargers /10/;

* represent the needs of each device at specific time.
integer variables ca_need_public(types, enter_hour, public_hour)
                  ca_need_quiet(enter_hour, quiet_hour)
                  ch_need_public(types, enter_hour, public_hour)
                  ch_need_quiet(enter_hour, quiet_hour)
                  lap_need_public(types, enter_hour, public_hour)
                  lap_need_quiet(enter_hour, quiet_hour);
ca_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"Calculator")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
ca_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"Calculator")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
ch_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"charger")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
ch_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"charger")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
lap_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"laptop")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
lap_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"laptop")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));

* declaration for split variables
integer variables                   
                  ca_need_public_1(types, enter_hour, public_hour)
                  ca_need_quiet_1(enter_hour, quiet_hour)
                  ch_need_public_1(types, enter_hour, public_hour)
                  ch_need_quiet_1(enter_hour, quiet_hour)
                  lap_need_public_1(types, enter_hour, public_hour)
                  lap_need_quiet_1(enter_hour, quiet_hour)
                  ca_need_public_2(types, enter_hour, public_hour)
                  ca_need_quiet_2(enter_hour, quiet_hour)
                  ch_need_public_2(types, enter_hour, public_hour)
                  ch_need_quiet_2(enter_hour, quiet_hour)
                  lap_need_public_2(types, enter_hour, public_hour)
                  lap_need_quiet_2(enter_hour, quiet_hour);
* ca_limit : limitation from total avaliable devices or limit concurrently exist object, ca_limit_quiet: limitation from calculator needs base
equation objective_refine, ca_limit_public, ca_limit_quiet, ch_limit_public, ch_limit_quiet, lap_limit_public, lap_limit_quiet,
        selection_ca_pub, selection_ca_quiet, selection_ch_pub, selection_ch_quiet, selection_la_pub, selection_la_quiet,
        ca_limit, ch_limit, la_limit, split_ca_pub, split_ca_quiet, split_ch_pub, split_ch_quiet, split_la_pub, split_la_quiet, split_limit_pub, split_limit_quiet;

* because we are maxmizing efficiency, so we only put calculate people to switch list if quiet_arrange is full
objective_refine..
    total_efficiency =e= sum((types, enter_hour, public_hour), (public_arrange(types, enter_hour, public_hour)+ ca_need_public_1(types, enter_hour, public_hour)*calculator_factor + ch_need_public_1(types, enter_hour, public_hour)*charger_factor + lap_need_public_1(types, enter_hour, public_hour)*laptop_factor)*eff_public(types, public_hour)
                                + (switch_p2q(types, enter_hour, public_hour) + ca_need_public_2(types, enter_hour, public_hour)*calculator_factor + ch_need_public_2(types, enter_hour, public_hour)*charger_factor + lap_need_public_2(types, enter_hour, public_hour)*laptop_factor)*eff_public(types, public_hour)*p2q) +
                         sum((enter_hour, quiet_hour), (quiet_arrange(enter_hour, quiet_hour) + ca_need_quiet_1(enter_hour, quiet_hour)*calculator_factor + ch_need_quiet_1(enter_hour, quiet_hour)*charger_factor + lap_need_quiet_1(enter_hour, quiet_hour)*laptop_factor)*eff_quiet(quiet_hour)
                                + (switch_q2p(enter_hour, quiet_hour)+ ca_need_quiet_2(enter_hour, quiet_hour)*calculator_factor + ch_need_quiet_2(enter_hour, quiet_hour)*charger_factor + lap_need_quiet_2(enter_hour, quiet_hour)*laptop_factor)*eff_quiet(quiet_hour)*q2p);
* this series of equations should be =g= because it is permitted that 4 people are permitted to come to the library but the library only have 3 calculators.
selection_ca_pub(types, enter_hour, public_hour)..
    sum((public_i)$(Public(public_i,"type")=ord(types)-1 and Public(public_i,"enter")=7+ord(enter_hour) and Public(public_i,"hours")=ord(public_hour) and Public(public_i,"Calculator") = 1), select_public(public_i)) =g= ca_need_public(types, enter_hour, public_hour);
selection_ca_quiet(enter_hour, quiet_hour)..
    sum((quiet_i)$(Quiet(quiet_i,"enter")=7+ord(enter_hour) and Quiet(quiet_i,"hours")=ord(quiet_hour) and Quiet(quiet_i,"Calculator") = 1), select_quiet(quiet_i)) =g= ca_need_quiet(enter_hour, quiet_hour);
selection_ch_pub(types, enter_hour, public_hour)..
    sum((public_i)$(Public(public_i,"type")=ord(types)-1 and Public(public_i,"enter")=7+ord(enter_hour) and Public(public_i,"hours")=ord(public_hour) and Public(public_i,"charger") = 1), select_public(public_i)) =g= ch_need_public(types, enter_hour, public_hour);
selection_ch_quiet(enter_hour, quiet_hour)..
    sum((quiet_i)$(Quiet(quiet_i,"enter")=7+ord(enter_hour) and Quiet(quiet_i,"hours")=ord(quiet_hour) and Quiet(quiet_i,"charger") = 1), select_quiet(quiet_i)) =g= ch_need_quiet(enter_hour, quiet_hour);
selection_la_pub(types, enter_hour, public_hour)..
    sum((public_i)$(Public(public_i,"type")=ord(types)-1 and Public(public_i,"enter")=7+ord(enter_hour) and Public(public_i,"hours")=ord(public_hour) and Public(public_i,"laptop") = 1), select_public(public_i)) =g= lap_need_public(types, enter_hour, public_hour);
selection_la_quiet(enter_hour, quiet_hour)..
    sum((quiet_i)$(Quiet(quiet_i,"enter")=7+ord(enter_hour) and Quiet(quiet_i,"hours")=ord(quiet_hour) and Quiet(quiet_i,"laptop") = 1), select_quiet(quiet_i)) =g= lap_need_quiet(enter_hour, quiet_hour);   
ca_limit(o)..
    sum((types, enter_hour, public_hour), ca_need_public(types, enter_hour, public_hour)$visible_public(o, enter_hour, public_hour)) + sum((enter_hour, quiet_hour), ca_need_quiet(enter_hour, quiet_hour)$visible_quiet(o, enter_hour, quiet_hour)) =l= calculators;
ch_limit(o)..
    sum((types, enter_hour, public_hour), ch_need_public(types, enter_hour, public_hour)$visible_public(o, enter_hour, public_hour)) + sum((enter_hour, quiet_hour), ch_need_quiet(enter_hour, quiet_hour)$visible_quiet(o, enter_hour, quiet_hour)) =l= chargers;    
la_limit(o)..
    sum((types, enter_hour, public_hour), lap_need_public(types, enter_hour, public_hour)$visible_public(o, enter_hour, public_hour)) + sum((enter_hour, quiet_hour), lap_need_quiet(enter_hour, quiet_hour)$visible_quiet(o, enter_hour, quiet_hour)) =l= laptops;
split_ca_pub(types, enter_hour, public_hour)..
    ca_need_public(types, enter_hour, public_hour) =e= ca_need_public_1(types, enter_hour, public_hour) + ca_need_public_2(types, enter_hour, public_hour);
split_ca_quiet(enter_hour, quiet_hour)..
    ca_need_quiet(enter_hour, quiet_hour) =e= ca_need_quiet_1(enter_hour, quiet_hour) + ca_need_quiet_2(enter_hour, quiet_hour);
split_ch_pub(types, enter_hour, public_hour)..
    ch_need_public(types, enter_hour, public_hour) =e= ch_need_public_1(types, enter_hour, public_hour) + ch_need_public_2(types, enter_hour, public_hour);
split_ch_quiet(enter_hour, quiet_hour)..
    ch_need_quiet(enter_hour, quiet_hour) =e= ch_need_quiet_1(enter_hour, quiet_hour) + ch_need_quiet_2(enter_hour, quiet_hour);
split_la_pub(types, enter_hour, public_hour)..
    lap_need_public(types, enter_hour, public_hour) =e= lap_need_public_1(types, enter_hour, public_hour) + lap_need_public_2(types, enter_hour, public_hour);
split_la_quiet(enter_hour, quiet_hour)..
    lap_need_quiet(enter_hour, quiet_hour) =e= lap_need_quiet_1(enter_hour, quiet_hour) + lap_need_quiet_2(enter_hour, quiet_hour);
split_limit_pub(types, enter_hour, public_hour)..
    ca_need_public_1(types, enter_hour, public_hour) + ch_need_public_1(types, enter_hour, public_hour) + lap_need_public_1(types, enter_hour, public_hour) =l= public_arrange(types, enter_hour, public_hour);
split_limit_quiet(enter_hour, quiet_hour)..
    ca_need_quiet_1(enter_hour, quiet_hour) + ch_need_quiet_1(enter_hour, quiet_hour) + lap_need_quiet_1(enter_hour, quiet_hour) =l= quiet_arrange(enter_hour, quiet_hour);
model simple_obj2 /conn1, conn2, limit, objective_refine, selection_ca_pub, selection_ca_quiet, selection_ch_pub, selection_ch_quiet, selection_la_pub, selection_la_quiet,
        ca_limit, ch_limit, la_limit, split_ca_pub, split_ca_quiet, split_ch_pub, split_ch_quiet, split_la_pub, split_la_quiet, split_limit_pub, split_limit_quiet,
        people_public, people_quiet, selection_quiet, selection_public, chatting_lower/;
solve simple_obj2 using mip maxmizing total_efficiency;

* save result in parameter
selection_public_("2", public_i) = select_public.l(public_i);
selection_quiet_("2", quiet_i) = select_quiet.l(quiet_i);
chairs("2", "public") = public_chair.l; 
chairs("2", "quiet") = quiet_chair.l;
Solver StatusModel StatusObjective#equ#varModel TypeSolverSolver Time
0Normal (1)Optimal Global (1)9830.48626426977MIPCPLEX0.067

Plot result at area below:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
%gams_pull -d chairs selection_public_ selection_quiet_
display(chairs)
chairs.set_index(['run'],inplace=True)
fig,(ax0,ax1) = plt.subplots(ncols=2,figsize=(14,5))
val=chairs.value.unique()
print(val)
labels=['public', 'quiet']
chairs.loc["1"].pivot_table(index=['room'],values=['value']).plot.pie(labels=labels,ax=ax1,y='value',legend=False)
ax0.pie(val,autopct='%1.2f',labels=labels)
ax0.set_ylabel('')
ax0.set_title('The number of students without calculation of equipments');
chairs.loc["2"].pivot_table(index=['room'],values=['value']).plot.pie(labels=labels,ax=ax1,y='value',legend=False)
ax1.pie(val,autopct='%1.2f')
ax1.set_ylabel('')
ax1.set_title('The number of students with calculation of equipments');
display(selection_public_, selection_quiet_)
runroomvalue
01public321.0
11quiet679.0
22public321.0
32quiet679.0
runpublic_ivalue
0111.0
1121.0
2131.0
3141.0
4151.0
............
2787219221.0
2788219231.0
2789219241.0
2790219251.0
2791219261.0

2792 rows × 3 columns

runquiet_ivalue
0111.0
1121.0
2131.0
3141.0
4151.0
............
3597218981.0
3598218991.0
3599219001.0
3600219011.0
3601219021.0

3602 rows × 3 columns

1
2
3
4
5
6
7
8
9
10
11
12
%%gams
total_limit = 50;
solve simple_obj1 using mip maxmizing total_efficiency;
selection_public_("1", public_i) = select_public.l(public_i);
selection_quiet_("1", quiet_i) = select_quiet.l(quiet_i);
chairs("1", "public") = public_chair.l; 
chairs("1", "quiet") = quiet_chair.l;
solve simple_obj2 using mip maxmizing total_efficiency;
selection_public_("2", public_i) = select_public.l(public_i);
selection_quiet_("2", quiet_i) = select_quiet.l(quiet_i);
chairs("2", "public") = public_chair.l; 
chairs("2", "quiet") = quiet_chair.l;
Solver StatusModel StatusObjective#equ#varModel TypeSolverSolver Time
0Normal (1)Optimal Global (1)704.9006014403MIPCPLEX0.019
1Normal (1)Optimal Global (1)791.63426426977MIPCPLEX0.086
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
%gams_pull -d chairs

#chairs.set_index(['run'],inplace=True)
display(chairs)
fig,(ax0,ax1) = plt.subplots(ncols=2,figsize=(14,5))
val=chairs.loc[chairs.run == "2"].value
vals=chairs.loc[chairs.run == "1"].value

labels=['public', 'quiet']
ax0.set_title('The number of students  without calculation of equipments');
ax0.pie(vals,autopct='%1.2f')
chairs.loc[chairs.run == "2"].pivot_table(index=['room'],values=['value']).plot.pie(labels=labels,ax=ax1,y='value',legend=False)
chairs.loc[chairs.run == "1"].pivot_table(index=['room'],values=['value']).plot.pie(labels=labels,ax=ax1,y='value',legend=False)
ax1.pie(val,autopct='%1.2f')
ax1.set_ylabel('')
ax1.set_title('The number of students with calculation of equipments');
runroomvalue
01public50.0
12public25.0
22quiet25.0

Conclusion for this part:

Based on our problem, (the total_limit is 1000), there are no significant difference between borrowing equipments and not borrowing equipments. But if we look into a smaller scalar problem, there are difference betweeen those two cases. The reason for it is that borrowing equipment has a low chance to happen.

For the conclusion, library need to arrange 321 seats for public area and 679 seats for quiet area in order to maxmize students’ total efficiency in the busy hours. We also demostrate a permission list but we think it is not unique and it is not as important as seats arrangement. So, we represented it but not discuss a lot about it.

Objective2:

More gdx file is provided. Those gdx files describe different time of requests from students. How to arrange seats in the library to try the best to meet the requirement of student’s thought in those gdx files and maximize the total efficiency of students using the library? Each gdx file is considered as a different scene, store the output in parameter and plot different seat arrangement during this year in a line diagram and draw out if there is any suggestion to provide to the library.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
%%gams
total_limit = 1000;
set obj2 "1:free 2:middle 3:busy" /1*3/;
parameter problem2(obj2, room), selection_problem2_quiet(obj2,quiet_i),  selection_problem2_public(obj2,public_i);

$onMultiR
$gdxin data-free.gdx
$load public_i<Public.dim1 public_j<Public.dim2 Public=Public
$load quiet_i<Quiet.dim1 quiet_j<Quiet.dim2 Quiet=Quiet
*,hours=hours,laptop=laptop,Calculator=Calculator, charger=charger;
$gdxin
n_pe_public(types, enter_hour, public_hour) = sum(public_i, 1$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
n_pe_quiet(enter_hour, quiet_hour) = sum(quiet_i, 1$((Quiet(quiet_i,"enter") = 7+ord(enter_hour)) and (Quiet(quiet_i,"hours") = ord(quiet_hour))));
ca_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"Calculator")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
ca_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"Calculator")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
ch_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"charger")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
ch_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"charger")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
lap_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"laptop")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
lap_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"laptop")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
solve simple_obj2 using mip maxmizing total_efficiency;
problem2("1", "public") = public_chair.l; 
problem2("1", "quiet") = quiet_chair.l;
selection_problem2_quiet("1", quiet_i) = select_quiet.l(quiet_i);
selection_problem2_public("1", public_i) = select_public.l(public_i);
Solver StatusModel StatusObjective#equ#varModel TypeSolverSolver Time
0Normal (1)Optimal Global (1)6809.38426425873MIPCPLEX0.05
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
%%gams
total_limit = 1000;
$onMultiR
$gdxin data-middle.gdx
$load public_i<Public.dim1 public_j<Public.dim2 Public=Public
$load quiet_i<Quiet.dim1 quiet_j<Quiet.dim2 Quiet=Quiet
*,hours=hours,laptop=laptop,Calculator=Calculator, charger=charger;
$gdxin
n_pe_public(types, enter_hour, public_hour) = sum(public_i, 1$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
n_pe_quiet(enter_hour, quiet_hour) = sum(quiet_i, 1$((Quiet(quiet_i,"enter") = 7+ord(enter_hour)) and (Quiet(quiet_i,"hours") = ord(quiet_hour))));
ca_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"Calculator")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
ca_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"Calculator")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
ch_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"charger")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
ch_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"charger")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
lap_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"laptop")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
lap_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"laptop")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
solve simple_obj2 using mip maxmizing total_efficiency;
problem2("2", "public") = public_chair.l; 
problem2("2", "quiet") = quiet_chair.l;
selection_problem2_quiet("2", quiet_i) = select_quiet.l(quiet_i);
selection_problem2_public("2", public_i) = select_public.l(public_i);
Solver StatusModel StatusObjective#equ#varModel TypeSolverSolver Time
0Normal (1)Optimal Global (1)8038.1826426342MIPCPLEX0.056
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
%%gams
total_limit = 1000;
$onMultiR
$gdxin data-busy.gdx
$load public_i<Public.dim1 public_j<Public.dim2 Public=Public
$load quiet_i<Quiet.dim1 quiet_j<Quiet.dim2 Quiet=Quiet
*,hours=hours,laptop=laptop,Calculator=Calculator, charger=charger;
$gdxin
n_pe_public(types, enter_hour, public_hour) = sum(public_i, 1$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
n_pe_quiet(enter_hour, quiet_hour) = sum(quiet_i, 1$((Quiet(quiet_i,"enter") = 7+ord(enter_hour)) and (Quiet(quiet_i,"hours") = ord(quiet_hour))));
ca_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"Calculator")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
ca_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"Calculator")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
ch_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"charger")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
ch_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"charger")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
lap_need_public.up(types, enter_hour, public_hour) = sum(public_i, Public(public_i,"laptop")$(Public(public_i,"enter") = 7+ord(enter_hour) and Public(public_i,"hours") = ord(public_hour) and Public(public_i,"type") = ord(types)-1));
lap_need_quiet.up(enter_hour, quiet_hour) = sum(quiet_i, Quiet(quiet_i,"laptop")$(Quiet(quiet_i,"enter") = 7+ord(enter_hour) and Quiet(quiet_i,"hours") = ord(quiet_hour)));
solve simple_obj2 using mip maxmizing total_efficiency;
problem2("3", "public") = public_chair.l; 
problem2("3", "quiet") = quiet_chair.l;
selection_problem2_quiet("3", quiet_i) = select_quiet.l(quiet_i);
selection_problem2_public("3", public_i) = select_public.l(public_i);
Solver StatusModel StatusObjective#equ#varModel TypeSolverSolver Time
0Normal (1)Optimal Global (1)9830.48626426977MIPCPLEX0.066

Plot result at area below:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
%gams_pull -d problem2 selection_problem2_quiet selection_problem2_public
import numpy as np
display(selection_problem2_quiet, selection_problem2_public);
display(problem2)
data = np.array(problem2.loc[problem2.room=="public"]).tolist()
public = list()
for i in data:
    public.append(i[2]);
data = np.array(problem2.loc[problem2.room=="quiet"]).tolist()
quiet = list()
for i in data:
    quiet.append(i[2]);
x = ["free", "middle", "bussy"]
plt.plot(x, public, marker='o', mec='r', mfc='w',label="public")
plt.plot(x, quiet, marker='*', ms=10,label="quiet")
plt.legend() 
plt.title("Seat arrangement for different time") 
plt.show()
obj2quiet_ivalue
0111.0
1121.0
2131.0
3141.0
4151.0
............
4620318981.0
4621318991.0
4622319001.0
4623319011.0
4624319021.0

4625 rows × 3 columns

obj2public_ivalue
0111.0
1121.0
2131.0
3141.0
4151.0
............
4603319221.0
4604319231.0
4605319241.0
4606319251.0
4607319261.0

4608 rows × 3 columns

obj2roomvalue
01public556.0
11quiet444.0
22public453.0
32quiet547.0
43public321.0
53quiet679.0

Conclusion for this part:

As we mentioned in the problem, we provided the permission in each case. But it is not useful.

By using the graph, we could clearly see that more quiet seats need to be arranged when students get bussier. This might be a guidance for library to provide different arrangement of seats in different time period.

Objective3:

Solve the model multiple times with different total seats provided, do you have any recommendation for the school that they need to buy more seats or not? Do not consider rules of fire protection design and construction of buildings. Plot the result in graph and explain the reason.

1
2
3
4
5
6
7
8
%%gams
set limits /1*200/;
parameter n_result(limits);
loop(limits,
     total_limit = ord(limits)*10;
     solve simple_obj2 using mip maxmizing total_efficiency;
     n_result(limits) = total_efficiency.l;
);
Solver StatusModel StatusObjective#equ#varModel TypeSolverSolver Time
0Normal (1)Optimal Global (1)165.59626426977MIPCPLEX0.11
1Normal (1)Optimal Global (1)331.18026426977MIPCPLEX0.089
2Normal (1)Optimal Global (1)488.79426426977MIPCPLEX0.084
3Normal (1)Optimal Global (1)642.63426426977MIPCPLEX0.085
4Normal (1)Optimal Global (1)791.63426426977MIPCPLEX0.085
...........................
195Normal (1)Optimal Global (1)10790.15826426977MIPCPLEX0.055
196Normal (1)Optimal Global (1)10790.15826426977MIPCPLEX0.054
197Normal (1)Optimal Global (1)10790.15826426977MIPCPLEX0.055
198Normal (1)Optimal Global (1)10790.15826426977MIPCPLEX0.054
199Normal (1)Optimal Global (1)10790.15826426977MIPCPLEX0.051

200 rows × 8 columns

Plot result area:
1
2
3
4
5
6
7
8
%gams_pull -d n_result
import pandas as pd
ax = plt.gca()
n_result.set_index(['value'],inplace=True)
for i in n_result["limits"]:
    n_result.replace(to_replace = i, value = int(i)*10, inplace=True) 
n_result.reset_index(inplace=True)
n_result.plot(kind='line',x='limits',y='value',ax=ax)

Conclusion for this part

As we could see on the graph that the slope goes down at point around 1200. So for the bussiest season, school do need to buy more chairs for students to study.

Conclusion for this project:

In this project, we learned how to use gams and solve a near real case problem. We observe an optimized seat arrangement for library to use. We also see the difference between different time in one semester and the result could be used to guide seat arrangements. At last, we see that 1000 seats might be too small for this library and they need to buy more.

We spent a lot of time on this project and we learned a lot from it. We also observe that gams system is pretty simple and efficient compared to other language. In the future, we would like to use it for more times on optimization problem.

 Previous

Java

 Comments