Energy simulation Javafx version

In a system where multiple types of energy source exist, running all components at all available times could be a waste by considering multiple different factors, including the device depreciation, normal energy in maintaining the entire system running. This waste is a significant factor when lower wind for wind producer happen, or lower light for light producer happen, or other stuff.

This is a javafx based energy running simulation simulator with choco-solver to find optimal threshold, which will be used to determine the time to turn on the device and time to turn off. It contains methods to analyze history data to predict a threshold to make the entire system running as efficient as it could. After proper data is provided, system will run based on a threshold setting from user or automatically analyzed based on history data so that no energy will be wasted. This app is done solely by me.

Ways of analyzing history data

If Using the first 30 input data to optimize and get the best possible threshold. is checked, the first 30 data will be used to generate the optimized threshold.

By comparing methods in passage Optimal Energy Production designed by me and the usage case, the following one is chosen at last:

Define variables

J : type of energy, $J\in$ {wind, water, $\cdots$ }

N : value index, 1, 2, $\cdots$.

C = $\mathbf{R}^J$: the normal energy consumption per unit time for each producer (Need to consider as a combination of multiple equipments, like: if we have two wind machine(user is able to define this in control), each machine will consume 10 W. Then $C_{wind}$=10*2=20)

U = $\mathbf{R}$: Total user consumption

W = $\mathbf{R}^{J,N}$, the expected energy(total in above table) produced in each value index, either pre-calculated or calculate in model.

S = {0,1}$^{J,N}$, to indicate I should turn on wind on this statistic data or not

B $\in \mathbf{R}$ : The battery charging limitation.

D $\in \mathbf{R}^{J,N}$, indicate the day count each value index, either pre-calculated or calculate in model.

Optimization Model

\begin{equation}\begin{split}&\text{Minimize } & \sum_{i\in N}\sum_{j\in J}D_{ij}S_{ij}\\& \text{Subject to}\ & 0 \le S_{ij} \le 1 \ \forall i\in N j\in J\\& & \sum_{i\in N}\sum_{j\in J}W_{ij}S_{ij}-\sum_{i\in N}\sum_{j\in J}C_{j}S_{ij}-U\ge B\end{split}\end{equation}

Use MIP to solve it

Code to solve it

By comparing with multiple different libraries to solve it, choco-solver is used on java platform at last, which is able to solve problems more than optimization and use machine learning in some cases. It is also able to solve other machine learning problems and provide a good way to customize based on different personal usage cases.

This code including reading data from stream, which better fits the real situation. Such that streaming data would be easily handled in the real situation. Details core code has multiple methods and it is visible at the Github repo.

Running

A easy way is to download the execution file from the publication page at Release, be caution that this is generated using Java, so only use it for study purpose.

Compile and run from source

The source code is located at https://github.com/ShaokangJiang/energy-javafx, it is tested to be working with JFoenix, choco-solver, JavaFX8, Java JDK.

NOT RECOMMEND as too many arguments, dependencies and it is easy to be wrong

Data format:

Simulation data

Header should be the same, User_Usage is not required but recommend. Each field represent the value sensor received.

Time,Wind_Speed,Light_H,Wave_Hight,Wave_Period,Current_Speed,User_Usage
0,5.405,1213.072,3.591,9.104,1.846,501.5935
0.2,8.157,1191.057,3.022,10.431,1.908,497.0755
0.4,6.012,1197.794,1.709,8.784,1.936,503.0145
0.6,6.477,1205.489,2.1,9.857,1.858,499.4511

Download a sample from here.

Optimization data

Header should be the same, idx is not required. Each category has a value component recoding the amount of power produced in unit time. Each count means the possibility of happening. Because we need to use a KWH = b KW * s/3600 to calculate energy produced. The count field has to be integer. We could use the possibility * a factor to make it become integer. And the sum of each count should be the same.

idx,wind_value,wind_count,light_value,light_count,wave_value,wave_count,current_value,current_count
0,4962654.905,189,100.8496541,45,485.3900022,222,71501.61128,105
1,424133.8855,45,105.8598321,124,328.6975665,43,49752.79798,187
2,3414695.961,18,113.1989172,130,438.1380705,33,35910.75581,12
3,7346795.761,90,116.4237558,11,483.7242291,24,48819.12566,25
4,4033868.032,20,105.5786618,25,226.1068017,14,1611.378029,35
5, , ,106.0583865,19,364.8009734,10,19265.12771,1

Download a sample from here.

Generate Fake Simulation and optimization data

Fake simulation data

Use java code below to generate fake simulation data(to be used in run page).

static Random r = new Random();
public static void main(String[] args) throws IOException {
  // TODO Auto-generated method stub
  FileWriter a = new FileWriter(new File("1.csv"));
  a.write("Wind_Speed,Light_H,Wave_Hight,Wave_Period,Current_Speed\r\n");
  double time = 0;
  while(time<36) {
    a.write(generateNormalVar(8,2)+","+generateNormalVar(1200,50)+
        ","+generateNormalVar(2.5,0.25)+","+generateNormalVar(9,0.5)+","+generateNormalVar(2,0.5)+"\r\n");
    time+=0.2;
  }
  a.flush();
  a.close();
}

/**
 * N(a,b)
 * center,distribution
 * @param x
 * @param y
 * @return
 */
public static String generateNormalVar(double a, double b) {
  double x = Math.sqrt(b)*r.nextGaussian()+a;
  r.nextGaussian();
  return String.format("%.3f", x);
}

Fake optimization data

• To make the input source be easy to manage, represent and maintain. We could save them in the same file, if no enough data for a cell, leave it empty would be fine and recommended.

• idx is not required but recommended

• This generation code might be good enough as this is not the real case

• header: idx,wind_value,wind_count,light_value,light_count,wave_value,wave_count,current_value,current_count

Use java code below to generate fake optimization data(to be used in start page):

public static void main(String[] args) throws IOException {
  FileWriter a = new FileWriter(new File("1.csv"));
a.write("idx,wind_value,wind_count,light_value,light_count,wave_value,wave_count,current_value,current_count\r\n");
  int count = 0;
  int year = 365;
  int wind_count=year,light_count=year,wave_count=year,current_count=year;
  while(wind_count>0 || light_count>0 || wave_count>0 || current_count>0 ) {
    int wind_count_=generateRandomIntegerIn(wind_count),light_count_=generateRandomIntegerIn(light_count),
        wave_count_=generateRandomIntegerIn(wave_count),current_count_=generateRandomIntegerIn(current_count);
    wind_count -= wind_count_;
    light_count -= light_count_;
    wave_count -= wave_count_;
    current_count -= current_count_;
    if(wind_count_==0&&light_count_==0&&wave_count_==0&&current_count_==0) continue;
    double Wind_Speed=generateRandomDoubleIn(4,15),Light_H=generateRandomDoubleIn(1100,1300),
        Wave_Hight=generateRandomDoubleIn(2,3),Wave_Period=generateRandomDoubleIn(7,11),
        Current_Speed=generateRandomDoubleIn(1,3);
    System.out.println(count+""+wind_count+""+light_count+""+wave_count+""+current_count+"");
    a.write(count + ","+ (wind_count_ == 0 ? " " : 2866*Wind_Speed*Wind_Speed*Wind_Speed) +","+(wind_count_ == 0 ? " " : wind_count_) +","+
          (light_count_ == 0 ? " " : 0.09*Light_H) +","+(light_count_ == 0 ? " " : light_count_) +","+
        (wave_count_ == 0 ? " " : 6.6*Wave_Hight*Wave_Hight*Wave_Period)+","+(wave_count_ == 0 ? " " : wave_count_)+","+
          (current_count_ == 0 ? " " : 1254*Current_Speed*Current_Speed*Current_Speed )+","+(current_count_ == 0 ? " " : current_count_)+"\r\n");
    count++;
  }
  a.flush();
  a.close();
}

//0~h
public static int generateRandomIntegerIn(int h) {
  return ThreadLocalRandom.current().nextInt(0, h + 1);
}

public static double generateRandomDoubleIn(int Min, int Max) {
  return Min + (Math.random() * ((Max - Min) + 1));
}

Usage

Each field means the threshold of each component except wave. In the case of wave, the threshold needs to be pre-calculated using $H^2T$. User usage is in kwh per day or unit time, the unit time refers to the refresh frequency, which will be used to calculate energy produced in the frame of time.

The way to calculate energy produced per unit time: a KWH = b KW*s/3600, a is the result, b is the current power, a is the calculated energy. s is the refresh frequency. Refresh frequency in this form is in ms(milliseconds).

In the manual setting, you are able to choose to provide user usage data in the future, usually this means to have a column of data recording user consumption per unit time, it will be used as a source of consumming power. If that file doesn't have user usage, you could set it at here. In the auto generate mode, you have to provide one to let us find the optimal solution(guess a possible one would be fine).

Calculation Equation

Wave: $P_{total}=0.6*11*H^2T=6.6H^2T$ H - height of wave T - period

Ocean Current: $P=\frac{\rho v^3 S C_p}{2}=\frac{1050 v^3 \pi1.3^2* 0.45}{2}=1254v^3$ P is the energy captured by the unit, ρ is the fluid density, V is the fluid velocity, and S is the swept area of the impeller$C_p$ is the energy utilization coefficient

Light: $P=\frac{798*H_A}{365*24}=0.09*H_A, H_A$ Total solar radiation per unit area

Wind: $P=\frac{\rho v^3 S C_p}{2}=\frac{1.293 v^3 9852* 0.45}{2}=2866v^3$ P is the energy captured by the unit, ρ is the fluid density, V is the fluid velocity, and S is the swept area of the impeller$C_p$ is the energy utilization coefficient

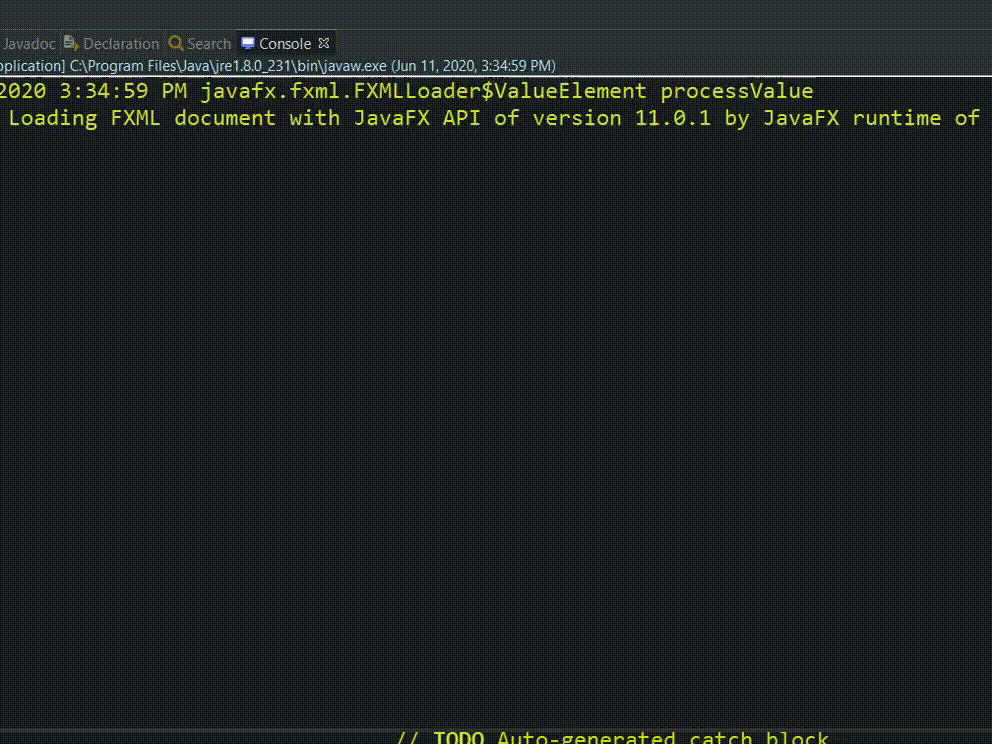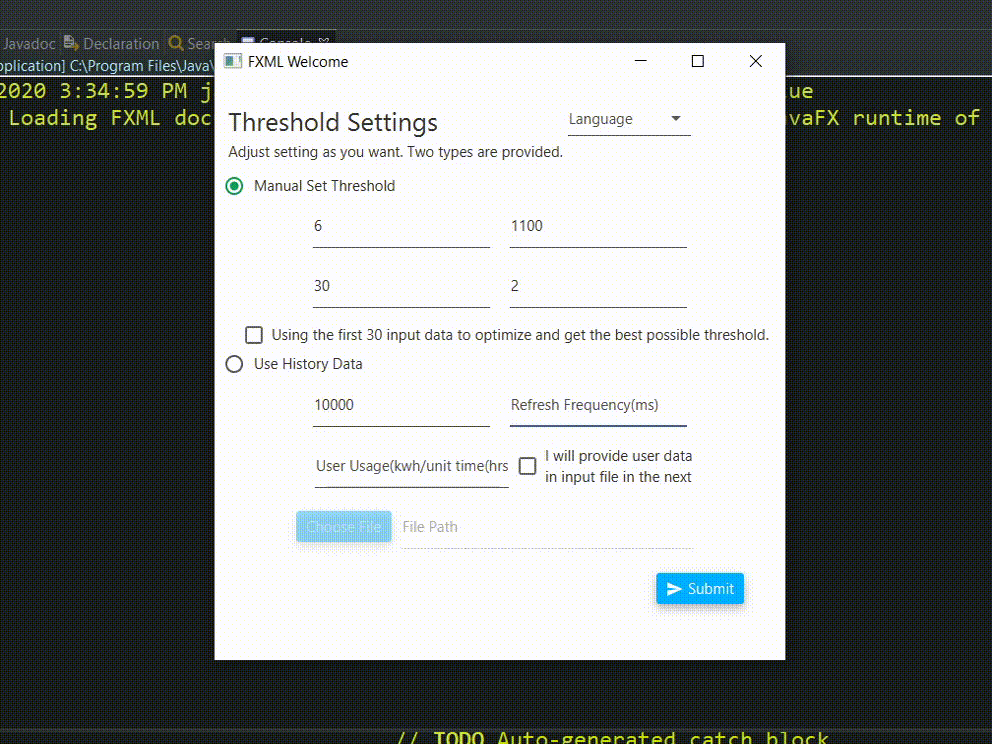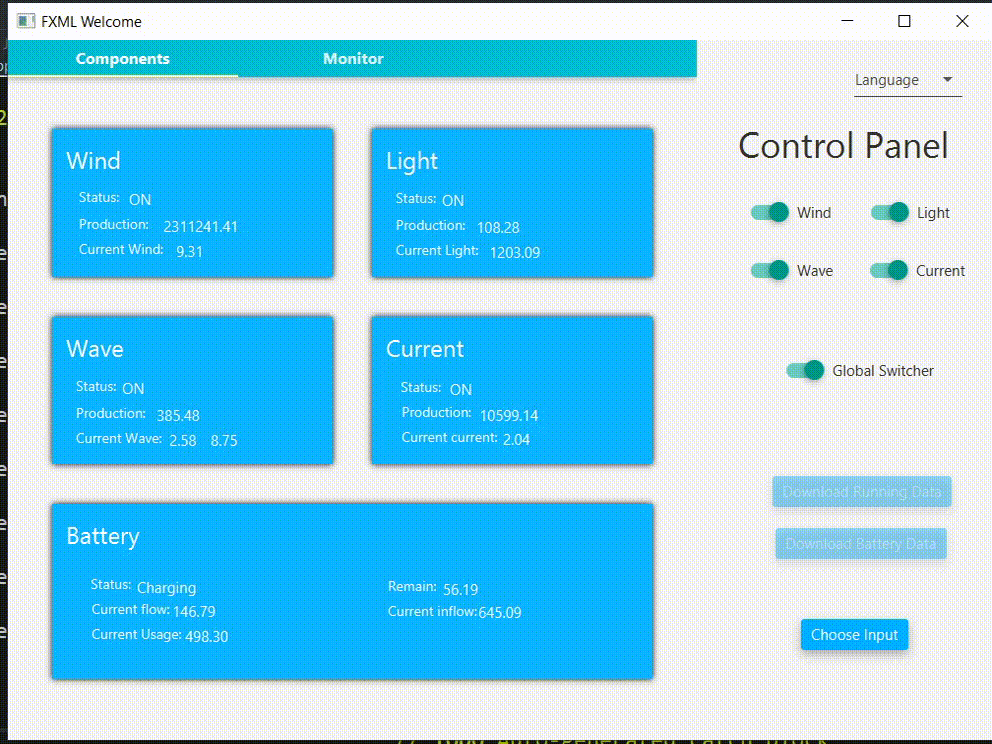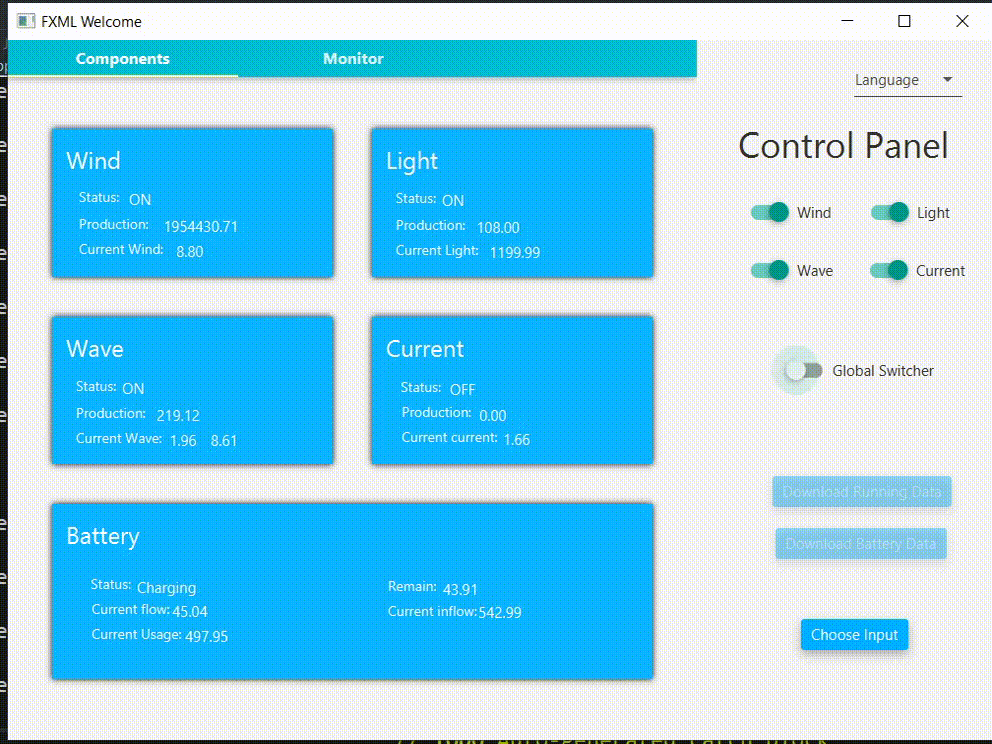
Sample running

Optimization is done automatically and is not shown in this demo.